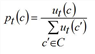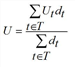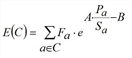Derived skims

Impedance of a connection = f (perceived journey time, fare, temporal utility). For the skim matrix you can select whether the temporal component should flow into the impedance in minutes or seconds.

Logsum of impedance. Can only be selected for timetable-based assignment and in conjunction with the "Logit" choice model. This skim is an alternative aggregation function for the "impedance” skim. The entries under "Aggregation" do not apply here. The logsum of the impedance for a demand time interval is defined by

LogSum = - 1/β • Ln Σv exp( -β • Wv ),

whereas V is totalized across all connections, Wv is the impedance of connection V, β of the choice model Logit parameters and Ln is the natural logarithm.

The skim for a relation is the weighted average across all demand time intervals, whereas the weight is the demand of the respective time interval. If independence is used, the definition changes to:

LogSum = -1/β • Ln Σv EIGAv • exp(β • Wv),

where EIGA_V represents the adjusted independence of connection V. The adjusted independence is calculated somewhat differently than the general case, also see chapter(Independence of connections). Instead of the general definition:

EIG_V = 1 / ( 1 + ∑i≠j wi(j) )

here

EIGA_V = 1 / ( 1 + ∑i≠j exp(-|Δt_i - Δt_j|) • wi(j) )

is used, whereas Δti is the time difference between the offered departure time and the desired departure time. In demand models, the logsum of impedance can be used instead of the impedance. An advantage of this skim is that an improvement in supply, for example when a connection is added, will never negatively impact the skim, which, in contrast, can happen with average impedance.

Note

When using independence in very specific combinations, adding a connection can lead to a slight deterioration of the skim.

Ratio of the journey distance and the journey time between origin and destination zone [km/h]

Journey speed [km/h] = journey distance [m] / 1,000) / journey time [min] / 60)

Ratio of the direct distance and the journey time between origin and destination zone [km/h]

Direct distance speed [km/h] = direct distance [m] / 1,000) / journey time [min] / 60)

Distance covered in the TSys as a percentage of the total in-vehicle distance of the connection

Skim which results from a user-defined formula according to the set parameters. The unit of the journey time equivalent of the calculated skims is determined by the user-defined formula.

The extended impedance is a component of the perceived journey time (PJT). It can be defined in the settings for the impedance of the timetable-based assignment and is thus only available in the timetable-based assignment.

The Utility is based on the following:

• On the one hand, the utility is based on C, which is the set of connections determined for an OD pair.
• On the other hand, the utility is based on the set of time intervals T = (t1, ..., tn) resulting from the time series relevant to the OD pair or from refined time series intervals, if applicable.

Per time interval t in T, each connection c in C has an impedance wt(c), which depends on t, since the impedance may contain the time interval’s distance from the connection’s departure time.

Using an antitone utility function f, the respective utility ut(c) is calculated from the impedance wt(c) according to ut(c) = f (wt(c)).

In case of the Logit model f(x) = e-bx.

The share of a connection c of the demand per interval t is then derived according to the following formula.

The denominator Ut is the overall utility of the time interval.

Compared to skims representing a mean value, Ut improves with every new connection that is added to the current transport supply.

For that reason the averaged Ut calculated over all time intervals is accounted for as a separate skim.

Here, dt is the total demand within time interval t.

Time during which a passenger has no seat in the course of this journey.

The skim is calculated as journey time weighted by vehicle journey item. Its weight is a function of the volume/seat capacity ratio.

For each individual PuT path C, the discomfort E(C) is defined as follows.

Here

a = Index over all vehicle journey items of a PuT path C

Fa = Journey time of the vehicle journey item a (known from its time profile)

Pa = Number of passengers on vehicle journey item a (over all paths, determined by assignment)

Sa = Number of seats on vehicle journey item a (based on the total of the seats of all vehicle journey sections which traverse the vehicle journey item on the respective calendar day)

A,B = free parameters

Path legs covered by a TSys of the PuT-Walk or PuT-Aux type in the PuT path are ignored.

Notes

• The discomfort due to capacity overload is only calculated with a timetable-based assignment.

Share of the passengers who are likely to experience a delay exceeding a specified threshold

The risk of delay per person is calculated as the weighted total of all transfers occurring in a relation and the risk of delay at the alighting destination.

Share of passengers denied boarding due capacity overload of vehicles